Introducing Commvault Cloud
Total Resilience.
No Exceptions.
Zero trust data security | Rapid, immutable recovery | The lowest TCO Commvault® Cloud, powered by Metallic® AI. It’s game-changing cyber resilience built to meet the demands of the hybrid enterprise.
The Platform
Your best defense against ransomware, at the best TCO
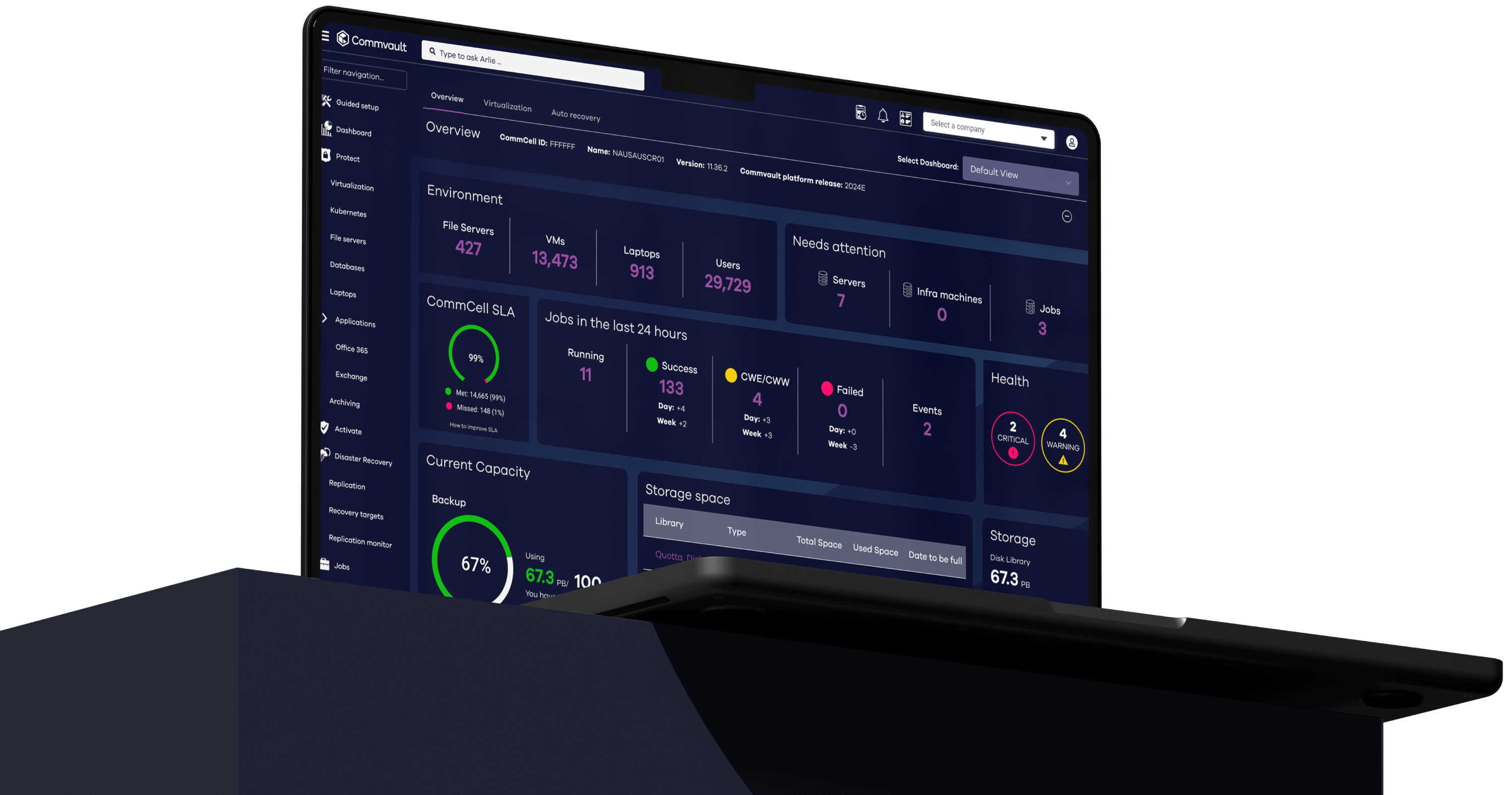
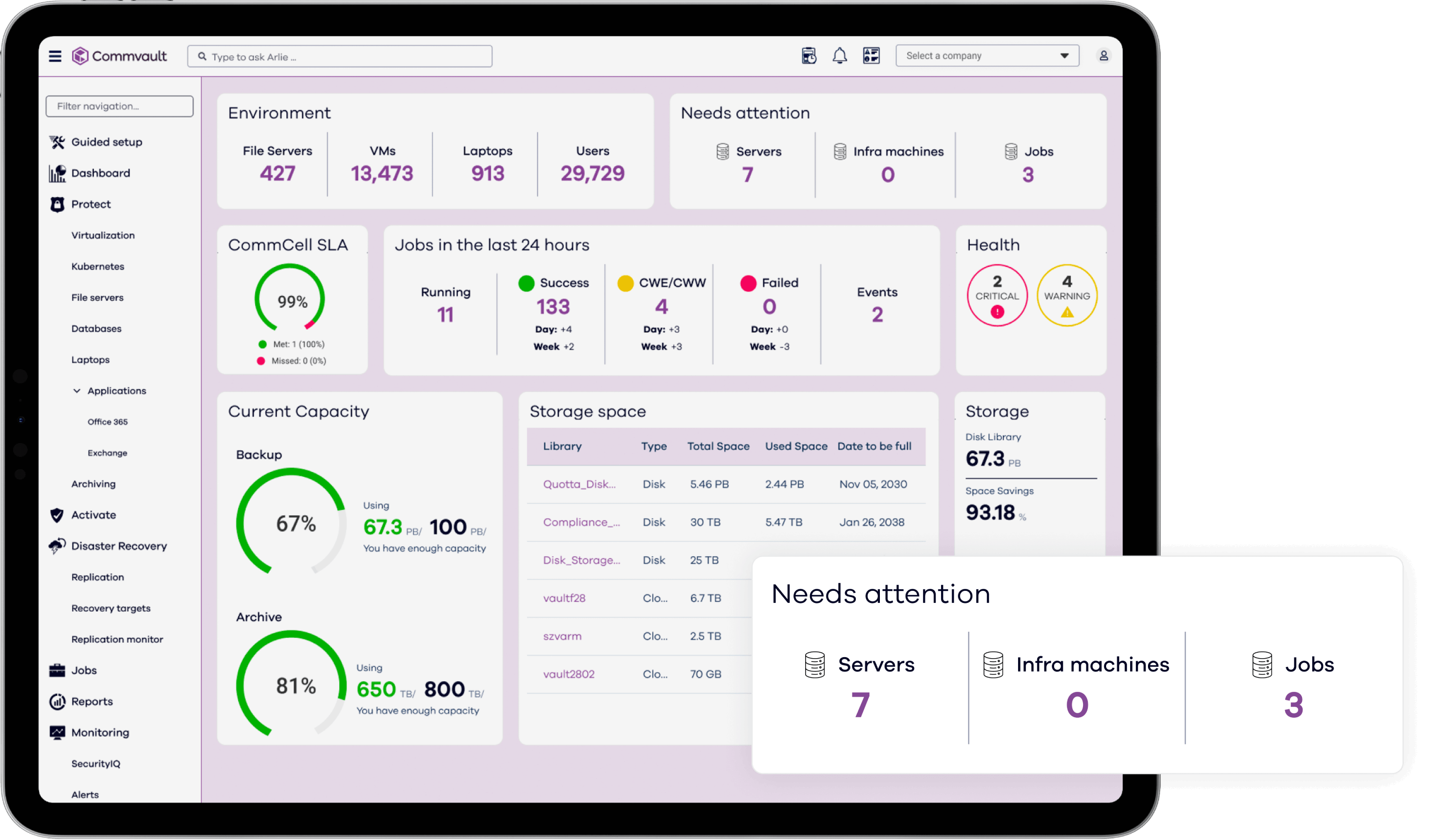
Commvault Cloud radically reduces the cost and complexity of protecting your business, all while delivering industry-leading advances in data security and cyber recovery, powered by advanced AI across the platform.
The industry’s best data security
The only platform built to secure data wherever it lives, with true cloud simplicity.
The industry’s most powerful AI: Metallic AI
Stop ransomware in its tracks with Metallic AI to monitor your data and predict and prevent attacks – plus automate a rapid, clean, immutable recovery if it’s ever needed.
The industry’s fastest cyber recovery
Only Commvault Cloud’s AI-driven automation gives you any-location recovery processing for the industry’s fastest recovery times, at massive scale, with the best TCO.
The industry’s lowest TCO
See, manage and recover data wherever it lives, from one, central cloud-based solution that eliminates silos and inefficiencies.

The Cyber Resilience guide
Learn why evolving threats demand an evolved approach to cyber resilience.
Commvault Cloud redefines cyber resilience. And expectations.
5x lower TCO
Better security, smarter budgeting.
15x reduction in management
Protecting all your data through a single pane.
True cloud data security
Cloud native – no appliances.
800% faster recovery
AI-powered recovery at cloud scale and speed.
Comprehensive Data Security
Comprehensive data security
No matter what you do or how you do it, Commvault Cloud delivers the most comprehensive data security—ensuring data protection everywhere your data resides, today and tomorrow.
Our reach
Supporting more than 100,000 companies






Related resources
Try it out







